部分题解在2020题解的帖子里,这里是剩余和今年更换后的题目的题解
| 题号 | 题目 | 类型 |
|---|---|---|
| 1160 | 猜数字 | 回溯 |
| 1167 | 逆序数(大数据) | 归并 |
| 1174 | 栈 | 栈 |
| 1179 | Shortest Path | 最短路 |
| 1186 | Tourist 2 | 回溯 |
| 1195 | Large Population | 最小生成树 |
| 1244 | Estrella’s Chocolate | 二分 |
| 1245 | Lisa’s Puzzle | 字典树 |
| 1250 | Bonus | 拓扑排序 |
| 1262 | Fish | 贪心 |
| 1264 | 字符不重复子串 | 两点 |
| 1269 | Craftman | 二分 |
| 1288 | Binary Search Tree | 二叉树 |
| 1289 | 3的倍数 | DP |
| 1291 | Buying Gifts | 排序,两点 |
| 1302 | Balance Tree | 二叉树 |
| 1303 | Sequence | dp |
| 1304 | ZUMA! | 模拟,递归 |
| 1305 | 斐波那契区间 | 两点 |
| 1347 | 消消乐 | 模拟,递归 |
| 1356 | Maze | 模拟 |
| 1370 | Ball | floyd |
| 1365 | Rotate | 枚举 |
| 1366 | Distance | 排序,两点 |
| 1367 | Min Base | 枚举,查找 |
| 1368 | substring | 两点 |
| 1369 | Black White Chess | bfs |
| 1378 | Blocks | 递推 |
1160 猜数字
枚举$N$的全排列(使用回溯或者STL的next_permutation方法),判断排列是否和询问的结果匹配。
1167 逆序数(大数据)
常见做法是归并排序或者树状数组、线段树来求。这里介绍归并排序的做法。
考虑归并排序时,合并时的两个子序列是有序的,不妨设为左右两个子序列,区间[left,mid-1]为左序列,区间[mid,right]为右序列,其中i指向左边子序列的待合并元素,j指向右边子序列的待合并序列。如果a[i]>a[j],那么也就意味着左序列中从[i,mid-1]的所有元素都会大于a[j],此时对于逆序数的贡献为mid - i。
所以我们只要稍微修改一下归并排序算法,就可以用来计算一个序列的逆序数,时间复杂度为$O(nlogn)$。
1174 栈
问题的核心时怎么能快速知道栈里的最小值,其他是栈的基本操作。
对于栈的元素,我们存两个值,一个是压栈元素的大小val,一个是以此元素为栈顶的栈的栈内元素最小值min。
当一个新值压栈时,与之前栈顶里的栈内元素最小值比较以来,来维护新栈顶的min。
这样查询最小值操作时,直接看栈顶的min值即可。
弹栈的时候,不需要额外操作。
所以压栈,弹栈,查最小值三个的操作时间复杂度都为$O(1)$。
所以总体时间复杂度为$O(M)$
1179 Shortest Path
首先,你要会写dijkstra算法求最短路,这个题朴素$(V^2)$的或者二叉堆优化的$ElogV$的都可以。
起点经过途中点到终点,依次为$c_1,c_2,\ldots,c_{k+2}$,依次求$c_i$到$c_{i+1}$的最短路,再把$c_i$删掉(不用真删,直接屏蔽掉就好)。
1186 Tourist 2
可以观察到$N$很小,最多为$9$,所以枚举$N$的全排列即可。 $O(N!)$
1195 Large Population
求最大生成树,由于生成树的边数一定是$N-1$,所以只要模仿最小生成树的做法即可。 题目给定的数据范围,用prim(时间复杂度为$O(V^2)$。)或者kruskal(时间复杂度为$O(ElogV)$)。都可以。
1244 Estrella’s Chocolate
题目是一个经典的求最小值最大问题的模型。
二分每天吃的热量最大值,对于这个热量,贪心求出多少天吃完这些巧克力。求二分值的下限。
时间复杂度为$O(Nlog(NM))$。
1245 Lisa’s Puzzle
按照数字二进制的逆序建立字典树(不过只有0和1,所以其实是个二叉树)。
字典树的节点上存有多少个数在建树时通过了这个节点。
再对于所有的数,进行字典树的查询即可。
样例对应的字典树为
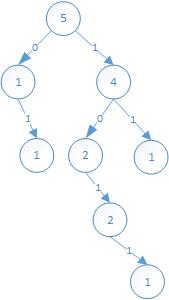
时间复杂度为$O(n)$。
1250 Bonus
有向图拓扑排序,如果存在环,那么所有人都是888;否则按拓扑序分层逆序推算。
核心代码
1 | int dfs(int u){ |
时间复杂度为$O(V+E)$。
1262 Fish
使用优先队列维护每次能钓到最多鱼的池塘,贪心求结果。注意,如果队头元素没有鱼或者鱼不会减少,那么就直接结束。时间复杂度为$O(nlogn)$。
1264 字符不重复子串
动态规划,用一个26的数组last记录最近一次出现字母的位置;一个字符串长度的数组len来记录第i个位置为后缀的最长不重复字符的长度。
对于位置i,len[i] = min{i-last[s[i]],len[i-1]+1}。
遍历字符串的过程中维护答案,求一个最大的len[i]即可。
时间复杂度为$O(n)$。
1269 Craftman
这题和1244 Estrella’s Chocolate是一个套路。
二分制作件数,检测需要的兑换券数量是否满足要求。
1288 Binary Search Tree
基于下面两个事实:
1. 二叉查找树的中序遍历就是排序结果
2. 二叉树的中序与前序,或者中序与后序可以唯一确定一棵二叉树。
所以,对于排列,进行二叉查找树的构建,然后做一次前序遍历,得到的序列作为这个二叉查找树的ID。
如果两棵二叉查找树的前序遍历序列相同,那么就是相同的,否则不同。
1289 3的倍数
递推
dp[i][j]表示前i个数码组成的数对三取模余数为j的方案数。
s[i] 表示第i个数码的值
k = s[i] % 3
那么 dp[i-1][j] 对 dp[i][j] 和 dp[i][(j+k)%3] 有贡献。
所以dp[i][:]只和dp[i-1][:]有关系,所以利用滚动数组来优化空间。
时间、空间复杂度都为$O(len)$。
1291 Buying Gifts
两点法,滑动窗口
先排序,然后用宽度为n的滑动窗口计算差价和总和。
总和计算不要每次都把窗口内的数加起来,利用相邻窗口总和的关系,去掉前一个,加后一个就可以了。
1302 Balance Tree
1. 先建树
2. dfs搜一遍,计算每个节点的左右子树的高度,判断是否平衡
1 | int dfs(int u){ |
建树的平均时间复杂度为$O(nlogn)$,最坏复杂度为$O(n^2)$;dfs的时间复杂度为$O(n)$。
也可以在建树的时候就维护每个节点为根的子树是否平衡,最后遍历一次所有节点,是否存在不平衡的节点。
1303 Sequence
经典的动态规划题目
dp[i][j]表示区间[i,j]取的最小代价。
dp[i][j] = min{dp[i][j-1]2+a[j], dp[i+1][j]2+a[i]}
1304 ZUMA!
模拟,递归。
枚举所有的位置,加入这颗新的珠子,模拟消除的过程(递归比较好写点),统计消除的珠子数量。
1305 斐波那契区间
两点法。
如果right位置满足Fibonacci要求,就一直向右延展;如果不满足,那么这个位置为新的left。这个过程中维护最长长度即可。
1347 消消乐
模拟
这个由于需要包含被交换的球,所以并不会发生连锁反应。
直接模拟,查找交换位置同颜色最左,最右的边界,再根据交换的球是否是同色分情况处理一下既可以。
1356 Maze
模拟
这个题并不是BFS,因为走的规则是一定,直接模拟走法,但是要注意判重,用一个数组vis[x][y][d],来存储格子(x,y)是否由d
方向进入过,如果出现重复那么就不可能走出来。
1370 Ball
floyd
1. 每个球是一个顶点,如果两个球称过,就连一条有向边。
2. 然后跑floyd,求可达矩阵。
3. 如果某个顶点的入度和出度相同,都是$\frac{n-1}{2}$,那么这个球即所求。
1365 Rotate
模拟
旋转外圈,不好写,换成旋转内圈。
枚举,统计一下就可。
1366 Distance
两点。
$O(n+m)$的暴力肯定会超时。
对A和B分别排序,然后类似于归并排序,两个点i和j分别指向数组A和B,哪边数值小,就移动一个,维护答案即可。
时间复杂度为$O(n+m)$
1367 Min Base
枚举,进制转换。
虽然n很大,但是随着基数b的增加,对应的位数是$log_{b}(n)的,所以,可以想象不用枚举多少次b,就能获得系数唯一。
所以枚举b,进制转换,记录系数,看是否是唯一的。
1368 substring
两点法。
用一个26的数组last记录对应字母上一次出现的位置。
先遍历字符串,计算是否达到了第一次所有字母都出现。
假设此时的位置为i,这时记录下此时last数组的最小值,那么初始答案为 i - min(last[:])
对于以后的每个字符,都执行上一步的操作,更新答案,直到字符串结束或者答案=26。
1369 Black White Chess
BFS
所有的局面为$2^{16}$个。
由全黑和全白的节点作为起始节点,BFS搜索出所有可达局面的最少步数,不可达的为-1。
对于每次查询,直接输出结果即可。
1378 Blocks
递推
dp[i][j][k] 为 i 列,共j个方块,末尾为k个方块的合法方案数
那么$ dp[i][j][k] = \sum_{t=1}^{k-1}{dp[i-1][j-k][t]} $
那么 $\sum_{k=1}^{n} {dp[m][n][k]}$ 为所求。
时间复杂度$O(n^3m)$
还可以优化到$O(n^2m)$,不过这个题本来也没想卡这个。

